这是一个本题的奇葩解法。
题目链接:https://www.luogu.com.cn/problem/P1351
### 思路分析 仔细观察这个题
我们可以发现一个令人振奋的结论:对于一个点,与它相连的其他所有点之间的距离恰恰是2
如果觉得有点难以理解,请看下图:
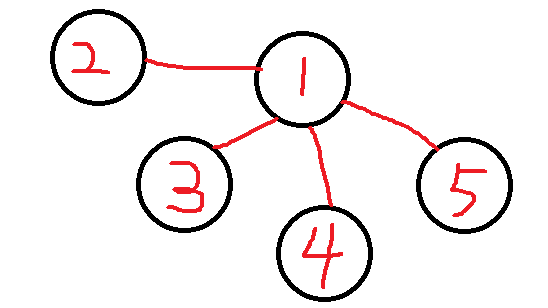 在这张图中,
在这张图中,2 到 3 的路径为
2->1->3
其他点也是类似的
因此 我们可以用一个 vector
储存所有点,再建一个数组表示这个点的权值 所以输入就解决了!
1
2
3
4
5
6
7
8
9
10
11
| vector <int> t[200002];
int tt[200002];
for(int i=0;i<n-1;i++){
int x,y;
cin>>x>>y;
t[x].push_back(y);
t[y].push_back(x);
}
for(int i=1;i<=n;i++){
cin>>tt[i];
}
|
接下来就是对每个点相连的点两两配对
计算联合权值的和,同时维护一个最大值
那怎么实现呢? 当然我们可以写两层 for
循环解决,类似于这样:
1
2
3
4
5
6
7
| for(int i=0;i<t[now].size();i++){
for(int j=i+1;j<t[now].size();j++){
sum=sum+tt[t[now][i]]*tt[t[now][j]*2;
sum%=10007;
maxx=max(maxx,sum);
}
}
|
但如果这样写的话,加上枚举每一个点,那就是3重循环了。现在请你想一想
有没有更好的办法呢?
主体代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| for(int i=1;i<=n;i++){
int pre=0;
mx1=0,mx2=0;
for(int j=0;j<t[i].size();j++){
int x=t[i][j];
tot=(tot+2*pre*tt[x])%10007;
pre=(tt[x]+pre)%10007;
if(tt[x]>mx1){
mx2=mx1;
mx1=tt[x];
}else if(tt[x]>mx2){
mx2=tt[x];
}
}
ans=max(ans,mx1*mx2);
}
|
至此,本题解决。
### 完整代码
上文已经分块讲好了思路,以下是完整代码(无注释,请确保在看懂上文后阅读):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| #include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long ll;
vector <int> t[200002];
int tot,ans,mx1,mx2,tt[200002];
int main(){
int n;
cin>>n;
for(int i=0;i<n-1;i++){
int x,y;
cin>>x>>y;
t[x].push_back(y);
t[y].push_back(x);
}
for(int i=1;i<=n;i++){
cin>>tt[i];
}
for(int i=1;i<=n;i++){
int pre=0;
mx1=0,mx2=0;
for(int j=0;j<t[i].size();j++){
int x=t[i][j];
tot=(tot+2*pre*tt[x])%10007;
pre=(tt[x]+pre)%10007;
if(tt[x]>mx1){
mx2=mx1;
mx1=tt[x];
}else if(tt[x]>mx2){
mx2=tt[x];
}
}
ans=max(ans,mx1*mx2);
}
cout<<ans<<" "<<tot;
return 0;
}
|
附上 DFS 解法
DFS比我的奇葩解法还慢了点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| #include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
vector <int> t[200005];
int tot,mx1,tt[200005];
void dfs(int x,int f) {
int pre=tt[f];
int mx2=pre;
int len=t[x].size();
for(int i=0; i<len; i++) {
int tmp=t[x][i];
if(tmp!=f) {
dfs(tmp,x);
tot=(tot+tt[tmp]*pre*2)%10007;
pre=(pre+tt[tmp])%10007;
mx1=max(mx1,tt[tmp]*mx2);
mx2=max(mx2,tt[tmp]);
}
}
}
int main() {
int n;
cin>>n;
for(int i=0; i<n-1; i++) {
int x,y;
cin>>x>>y;
t[x].push_back(y);
t[y].push_back(x);
}
for(int i=1; i<=n; i++) {
cin>>tt[i];
}
dfs(n,0);
cout<<mx1<<" "<<tot;
return 0;
}
|
 在这张图中,
在这张图中,